Największy wspólny dzielnik (NWD)
Temat: Największy wspólny dzielnik (NWD).
Największy wspólny dzielnik (NWD) to największa liczba naturalna przez którą możemy podzielić dowolną parę liczb całkowitych w taki sposób aby z dzielenia nie została reszta.
Aby wyznaczyć NWD dwóch liczb, rozkładamy każda z nich na czynniki pierwsze, wypisujemy te czynniki, które powtórzyły się w obu rozkładach i obliczamy ich iloczyn.
Zanim przejdziemy do wyznaczania NWD przypomnijmy sobie na czym polega rozkład liczby na czynniki pierwsze. Aby go wykonać należy zastosować poniższe kroki:
- Zapisujemy liczbę, którą chcemy rozłożyć na czynniki pierwsze.
- Rysujemy pionową kreskę po prawej stronie liczby.
- Dzielimy tę liczbę przez najmniejszą liczbę pierwszą, która będzie jednocześnie jej dzielnikiem. Dzielnik zapisujemy po prawej stronie a wynik tego dzielenia po lewej (pod liczbą, którą dzieliliśmy)
- Operację z poprzedniego podpunktu powtarzamy tak długo (dzielimy przez liczby pierwsze) aż w wyniku dzielenia uzyskamy 1.
Zadanie 1
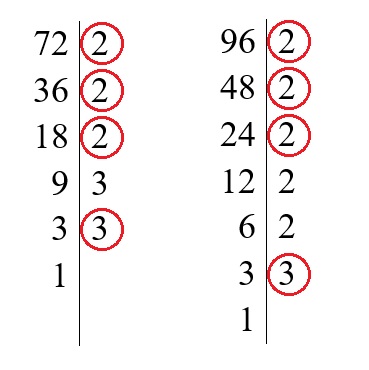
Rozłóż podane liczby na czynniki pierwsze:
ROZWIĄZANIE:
WSKAZÓWKI:
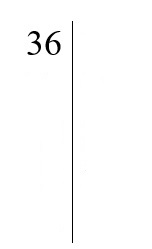
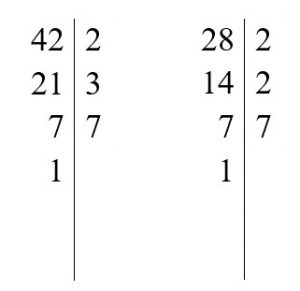
1. Zapisujemy liczbę 36 i rysujemy pionową kreskę po prawej stronie.
2. Dzielimy liczbę 26 przez najmniejszą liczbę pierwszą ( w tym przypadku dzielimy liczbę 36 przez 2, ponieważ 26 jest podzielna przez 2). Dzielnik czyli liczbę przez którą dzielimy zapisujemy po prawej stronie kreski, zaś wynik tego dzielenia czyli liczbę 18 zapisujemy po lewej stronie pod liczbą 36.
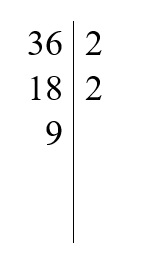
3. Analogicznie postępujemy z liczbą 18. Dzielimy ją przez najmniejszą liczbę pierwszą ( liczba 18 także podzieli się na 2 ). Liczbę przez którą dzielimy zapisujemy po prawej stronie kreski a wynik tego dzielenia (liczbę 9) zapisujemy po lewej stronir pod liczbą 18.
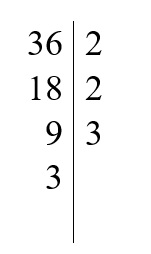
4. Postępujemy tak samo z liczbą 9 – czyli dzielimy ją przez najmniejszą liczbę pierwszą . Liczba 9 nie dzieli się przez 2, więc bierzemy kolejną liczbę pierwszą – liczbę 3. Liczba 9 jest podzielna przez 3 więc wykonujemy dzielenie. Dzielnik zapisujemy po prawej stronie a wynik dzielenia po lewej pod liczbą 9.
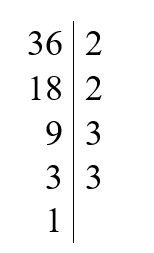
5. Otrzymaną liczbę – 3 również dzielimy przez najmniejszą liczbę pierwszą czyli przez 3. Dzielnik zapisujemy po prawej stronie kreski a wynik – czyli liczbę 1 zapisujemy po lewej stronie. W tym momencie zakończyliśmy rozkład, ponieważ dostaliśmy liczbę 1.
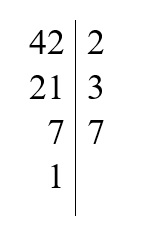
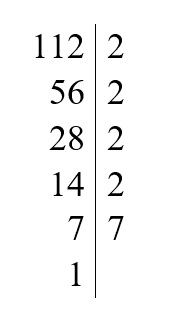
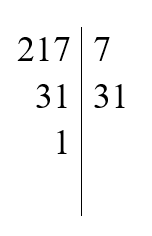
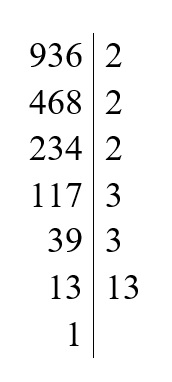
Zadanie 2
Oblicz NWD podanych liczb:
ROZWIĄZANIE:
WSKAZÓWKI:
1. Rozkładamy każdą z liczb na czynniki pierwsze.
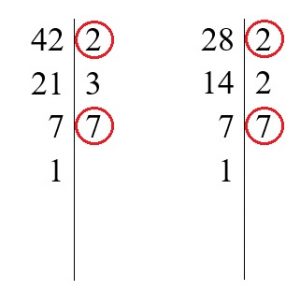
2. Zaznaczamy czynniki ( liczby po prawej stronie), które powtórzyły się w obu rozkładach. Można zaznaczyć kółeczkiem jak na rysunku obok.
3. Z każdej pary liczb zapisujemy tylko jedną liczbę ( z pary dwójek zapisujemy jedną dwójkę i z pary siódemek zapisujemy jedną siódemkę) i mnożymy je przez siebie (obliczamy ich iloczyn).
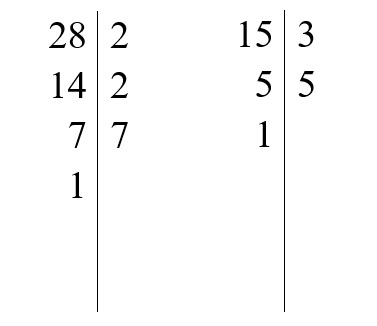
Liczby 28 i 15 nie mają wspólnych czynników pierwszych. W związku z tym ich jedynym wspólnym dzielnikiem jest liczba 1. Takie liczby nazywamy liczbami względnie pierwszymi.
Course Features
- Lectures 0
- Quizzes 0
- Duration 50 hours
- Skill level All levels
- Language English
- Students 0
- Assessments Yes